Codeforces.com-да тапсырма орындау
Графтар және олимпиадаға дайындық
Графтар туралы ақпарат
Графтар туралы алғашқы мәліметтер XVIII ғасырда пайда болды. Олар белгілі бір түзулер мен сызықтар арқылы өзара байланысқан нүктелердің жиынтығы ретінде түсіндірілді. Алғашқыда бұл мәліметтер көбінесе ойындар мен логикалық жұмбақтар түрінде қолданылды. Дегенмен, XIX ғасырдың соңында топология саласының дамуы графтар теориясына деген қызығушылықты арттырды. Бүгінде графтар теориясының әдістері көптеген салаларда, соның ішінде әлеуметтану, экономика, биология, медицина, химия, психология, сондай-ақ дискретті математика мен бағдарламалау сияқты бағыттарда пайдаланылады. Көптеген қолданбалы есептерде әртүрлі объектілер арасындағы байланыстарды зерттеу қажет болады. Осы мәселелерді геометриялық тәсілмен шешу графтар теориясы деп аталады.
Граф — бұл математикалық құрылым, ол нүктелер (немесе төбелер) мен оларды қосатын түзулерден (немесе қабырғалардан) тұрады. Графты кейде объектілер мен олардың арасындағы байланыстарды сипаттау үшін қолданады.
Графтың негізгі элементтері:
- Төбелер (немесе нүктелер): Графтың негізгі элементтері, олар объектілерді немесе түйіндерді білдіреді.
- Қабырғалар (немесе түзулер): Төбелер арасындағы байланыстарды білдіреді. Әрбір қабырға екі төбені қосады.
Графтар екі түрге бөлінеді:
- Бағытталмаған граф: Қабырғалар арасында ешқандай бағыт болмайды, яғни олар екі төбе арасында екіжақты байланыс құрайды.
- Бағытталған граф: Қабырғалар арасында бағыт бар, яғни әр қабырға бір төбеден екінші төбеге қарай бағытталған.
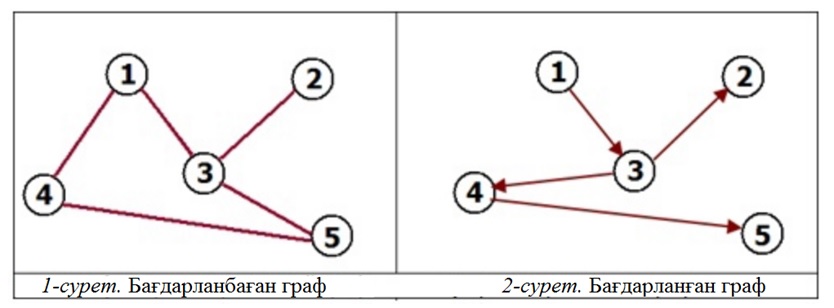
Жазықтықта әртүрлі бес нүкте орналастырайық (1-сурет). Бұл нүктелер графтың төбелері деп аталады, ал оларды қосатын сызықтар графтың қабырғалары болып табылады. Егер графтың барлық қабырғалары бағытталмаған болса, онда оны «бағытталмаған граф» деп атайды (1-сурет). Ал егер графтың барлық қабырғалары бағытталған болса, онда ол «бағытталған граф» деп аталады (2-сурет).
Графтар теориясы түрлі салаларда, мысалы, компьютер ғылымында, әлеуметтік желілерде, көлік жүйелерінде және көптеген басқа ғылымдарда кеңінен қолданылады.
Флойд алгоритмі
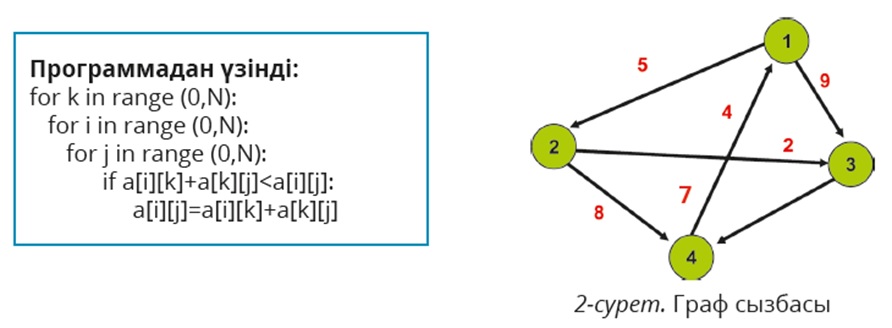
Толық бағдарланған қабырғаларының салмағы көрсетілген және байланыс матрицасы арқылы сипатталатын граф үшін ең қысқа жолдарды анықтауға арналған. Қабырғалардың салмағы 100-ден аспайды.
Алгоритмнің негізі — графтың кез келген екі төбесі арасындағы ең қысқа жолды табу. Мысалы, 1-төбеден 3-төбеге ең қысқа жолдың ұзындығы 7-ге тең: (1, 3) = 7, ал 3-төбеден 1-төбеге (3, 1) = 11 болады (бағдарланған графты қарастыра отырып).
| INPUT.TXT | OUTPUT.TXT |
| 4 0 5 9 100 100 0 2 8 100 100 0 7 4 100 100 0 |
0 5 7 13 12 0 2 8 11 16 0 7 4 9 11 0 |
Тапсырмалар:
- Графта тереңдігінен іздеу алгоритмін жүзеге асыратын программа құру.
- Графта көлденеңінен іздеу алгоритмін жүзеге асыратын программа құру.
- Графтың берілген төбесінен d қашықтықта орналасқан барлық төбелерін анықтау үшін көлденеңінен іздеу алгоритмін қолдану.
A есеп. Қалалар мен жолдар
(Уақыты: 5 сек. Жад: 16 МБ)
Нептун планетасындағы Құс жолы галактикасында N қала бар, олардың кейбіреулері жолдармен байланысты. Құс жолы галактикасының императоры «Максимус» «Нептун» планетасындағы жолдарды түгендеу туралы шешім қабылдады. Бірақ оның математикадан жақсы емес екені белгілі болды, сондықтан ол сізден жолдардың санын санауды сұрайды.
Деректерді енгізу
Бірінші жол N санын көрсетеді (0 ≤ N ≤ 100). Келесі N жолдарда әрқайсысы бір немесе нөл болатын N сандар бар . Оның үстіне шаршы матрицаның (i , j) орнында біреу болса , онда i - ші және j - ші қалалар жолдар арқылы қосылады, ал нөл болса, онда олар қосылмайды.
Басып шығару
Бір санды шығарыңыз - «Нептун» планетасындағы жолдар саны.
| INPUT.TXT | OUTPUT.TXT |
| 5 0 1 0 0 0 1 0 1 1 0 0 1 0 0 0 0 1 0 0 0 0 0 0 0 0 |
5 |
В есеп. Түрлі түсті жаңбыр
(Уақыты: 5 сек. Жад: 16 МБ)
Банан Республикасында көпірлермен байланыстырылған көптеген төбелер бар. Химия зауытында «Зован» тәжірибелік тыңайтқышы булану салдарынан апат орын алды. Келесі күні түрлі-түсті жаңбыр жауды, бірақ ол тек төбеден жауды. Кейбір жерлерде тамшылар қызыл, кейбір жерлерде көк, ал басқаларында жасыл болды, бұл төбелердің сәйкес түске айналуына себеп болды. Бұл Банан Республикасының Президентіне ұнады, бірақ ол төбелердің арасындағы көпірлерді бояғысы келді, осылайша көпірлер олар байланыстыратын төбелердің түсіне боялады. Өкінішке орай, төбелердің түсі әртүрлі болса, көпірді бұлай бояу мүмкін емес. Осындай «жаман» көпірлердің санын есептеңіз.
Деректерді енгізу
Кіріс деректерінің бірінші жолында N (0 < N ≤ 100) саны – төбелер саны бар. Одан кейін төбелер арасындағы көпірлердің болуын сипаттайтын іргелес матрица келеді (1 – көпір бар, 0 – жоқ). Көршілес матрицадан кейін бос жол бар , ал соңғы жолда төбелердің түсін көрсететін N саны бар: 1 – қызыл; 2 – көк; 3 – жасыл.
Басып шығару
Бір санды шығарыңыз - «нашар» көпірлер саны.
| INPUT.TXT | OUTPUT.TXT |
| 7 0 1 0 0 0 1 1 1 0 1 0 0 0 0 0 1 0 0 1 1 0 0 0 0 0 0 0 0 0 0 1 0 0 1 0 1 0 1 0 1 0 0 1 0 0 0 0 0 0 1 1 1 1 1 3 3 |
4 |
C есеп. Қалалар мен жолдар
(Уақыты: 5 сек. Жад: 16 МБ)
Зынданда M туннель және N қиылысу бар , әрбір туннель екі қиылысты байланыстырады. Тышқан патшасы әр қиылыс алдында әрбір туннельге бағдаршам орнатуды ұйғарды. Әр қиылыста қанша бағдаршам орнату керектігін есептейтін программа жазыңыз. Қиылыстар 1-ден N- ге дейін нөмірленеді.
Деректерді енгізу
Енгізудің бірінші жолында N және M екі саны бар (0 < N ≤ 100, 0 ≤ M ≤ N *( N – 1)/2). Келесі M жолының әрқайсысында i және j (1 ≤ i , j ≤ N ) екі сандары бар , бұл i және j қиылысулары туннель арқылы қосылғанын білдіреді.
Басып шығару
N сандарды шығару қажет : k - ші сан k - ші қиылысындағы бағдаршамдардың санын білдіреді .
Ескерту : Кез келген екі қиылыс бір туннельден аспайтындай жалғасады деп болжауға болады. i түйісуінен оның өзіне дейінгітуннельдер жоқ.
| INPUT.TXT | OUTPUT.TXT |
| 7 10 5 1 3 2 7 1 5 2 7 4 6 5 6 4 7 5 2 1 5 3 |
3 3 2 2 5 2 3 |
Қорытынды
Қорытындылай келе, Python бағдарламалау тілінің негіздерінен бастап, күрделі тақырыптарға дейін көптеген тапсырмаларды орындауға болады. Python тілінің синтаксисі қарапайым әрі оқуға жеңіл, бұл оны бағдарламалауды үйренушілер үшін өте қолайлы етеді.